Finding good information on how filters work, what the different types of filters mean, and how you should filter your data is hard. Lots of explanations only make sense if you have a year or two of electrical engineering education, and most of the rest are just a list of rules of thumb. I want to try to get you to a place where you can test your own filter settings, and show you the importance of the rules of thumb without going into the relatively complex math that is often used to explain filters. Warning: a lot of the code I’m going to use requires the Matlab Signal Processing Toolbox. If you don’t have it, you wont be able to execute the code yourself, but hopefully you’ll still be able to follow along with the logic.
What is a filter?
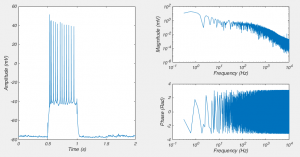
Fig 1. On the left is a recording from a neuron shown in the “time domain”. The two graphs on the right show the same recording in the “frequency domain”
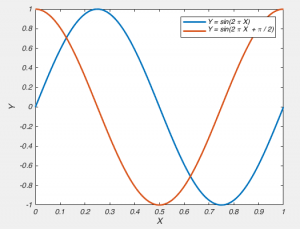
Fig 2. A graph of Y = sin(2π X) and a graph of Y = sin(2πX + π/2) have the same frequency components, but different phases
There are a huge variety of filters, but one of the simplest ways of dividing them up is to consider what signals they don’t affect, i.e. what signals they let pass through them. So a low-pass filter lets through low frequency signals and a high-pass filter lets through high frequency data. There are also band-pass filters which only let through signals in a particular frequency range and to break convention, band-stop filters, which stop signals inside a particular frequency range. The frequency at which the signal begins to be filtered is called the “corner frequency” or the “cut-off frequency”. When we describe the actions of a filter, we are often show it’s frequency response, which is shows you what the filter does to various frequency components of your data. This can be estimated by applying the filter to your data, viewing it in the frequency domain and then dividing that by your original signal in the frequency domain. However, as your data doesn’t usually contain all frequency components, it better to create white noise, which is a signal that has the same amount of power in all frequency components. We can convert data to the frequency domain by using the Fourier transform (which I’ve talked about before here). In code, that looks like this.
signal = randn(1000,1); %Create white noise
dt = 0.5; %dt is the time between samples
time = 1:dt:1000 ; %create time base
%% Filter the data
%Make a simple running average filter
%Take the mean of the original data in a window
%of the data tempC(i:i+window)
%I know there are faster ways of doing this.
tempC_filt = zeros(size(signal));
window = 5;
for i = 1:length(signal)
end_idx = i+window;
if end_idx > length(signal)
end_idx = length(signal);
end
tempC_filt(i) = mean(signal(i:end_idx));
end
%% Now convert data to frequency domain
nfft = 2^nextpow2(length(signal)); %FFTs are faster if you perform them
%on power of 2 lengths vectors
f = (1/dt)/2*linspace(0,1,nfft/2+1)'; %Create Frequency vector'
dft = fft(signal, nfft)/(length(signal)/2); % take the FFT of original
dft_filt = fft(tempC_filt, nfft)/(length(tempC_filt)/2); %take FFT of filters
mag = abs(dft(1:nfft/2+1)); %Calculate magnitude
mag_filt = abs(dft_filt(1:nfft/2+1)); %Calculate magnitude
loglog(f, mag_filt./mag)
xlabel('Frequency (Hz)')
ylabel('Signal Out / Signal In')
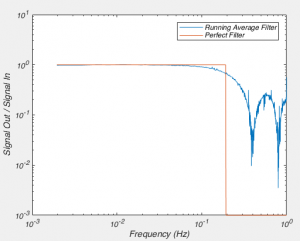
The above code produces the graph in figure 3, which shows the the frequency components of the filtered signal divided by the frequency component of the original signal. What it shows us is that the running average filter doesn’t affect signals below 10^-1 Hz (0.1 Hz), but attenuates them above that. It also shows us that a running average filter doesn’t uniformly attenuation signals above 0.1 Hz, but instead filters out signals more strongly at about 0.4 Hz and 0.8 Hz than it does at 0.6 Hz and 1 Hz. This problem is refereed to as “ripples in the stop band”, where the “stop band” is the region of frequencies where the signal is attenuated, and “ripples” are the changing amount of attenuation of your signal with frequency. Compare this the “perfect” filter, where the signal is not attenuated at all up until some frequency, and then the signal is completely obliterated beyond that (I know it’s shown as only being attenuated by 10^-3, but you can’t show 0 on a log axis). This “perfect” filter is what most filters want to be. They want to not alter the signal in frequency ranges of the “pass band”, and completely remove the signal in the stop band. But filters like that are impossible to create in real life.
Now I’ve said a perfect filter doesn’t want to alter signals in the pass-band, and by looking at the graph above, it might appear that so long as you are below about 0.1 Hz you wont affect the signal, but as I alluded to before, we need to consider what the filter does to the phase. We can achieve that by adding only a few more lines to our above code.
signal = randn(1000,1); %Create random time series data
dt = 0.5; %dt is the time between samples
time = 1:dt:1000 ; %create time base
%% Filter the data
%Make a simple running average filter
%Take the mean of the original data in a window
%of the data tempC(i:i+window)
%I know there are faster ways of doing this.
tempC_filt = zeros(size(signal));
window = 5;
for i = 1:length(signal)
end_idx = i+window;
if end_idx > length(signal)
end_idx = length(signal);
end
tempC_filt(i) = mean(signal(i:end_idx));
end
%% Now convert data to frequency domain
nfft = 2^nextpow2(length(signal)); %FFTs are faster if you perform them
%on power of 2 lengths vectors
f = (1/dt)/2*linspace(0,1,nfft/2+1)'; %Create Frequency vector'
dft = fft(signal, nfft)/(length(signal)/2); % take the FFT of original
dft_filt = fft(tempC_filt, nfft)/(length(tempC_filt)/2); %take FFT of filters
mag = abs(dft(1:nfft/2+1)); %Calculate magnitude
mag_filt = abs(dft_filt(1:nfft/2+1)); %Calculate magnitude
phase = angle(dft(1:nfft/2+1));
phase_filt = angle(dft_filt(1:nfft/2+1));
%% Create an ideal filter frequency response
mag_perf = ones(size(mag_filt));
mag_perf(100:end) = 10^-3;
subplot(1,2,1)
loglog(f, mag_filt./mag, f, mag_perf)
xlabel('Frequency (Hz)')
ylabel('Signal Out / Signal In')
legend('Running Average Filter', 'Perfect Filter')
subplot(1,2,2)
semilogx(f, unwrap(phase-phase_filt));
xlabel('Frequency (Hz)')
ylabel('Phase Shift (Rad)')
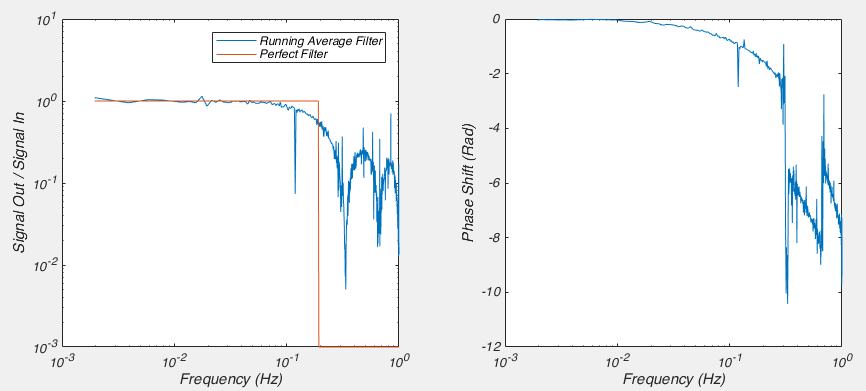
Here we can clearly see that the phase of the signal is being affected at frequencies as low as 0.05 Hz. So while the amplitude of these frequency components isn’t being changed, they are being shifted later in time. So this is not a particularly good filter. Let’s move on in our quest to both understand, and create a better filter.
Filter Poles
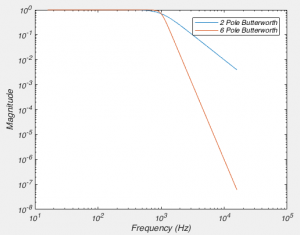
(From here on in, I’m only going to be talking about low-pass filters, as everyone uses them. But everything I say is applicable to high-pass filters too)Another way of describing a filter is by the number of “poles” it has. I’m not going to explain to you what a pole is, because it comes from the mathematical analysis of filters, and ultimately, it is irrelevant for understanding what the consequence of the filter is. Simply put a filter with more poles attenuates frequencies more heavily for each Hz you go up. Here a figure will paint a thousand words, so see fig 5. We can create that figure with the below code.
%All our filters will have a corner
%frequence (fc) of 1000 Hz
fc = 1000; % Corner Frequency of
[b2pole,a2pole] = butter(2,2*pi*fc,'s'); %Create a 2 pole butterworth filter
[h2pole,freq2] = freqs(b2pole,a2pole,4096); %Calculate Frequency Response
[b6pole,a6pole] = butter(6,2*pi*fc,'s'); %Create a 2 pole butterworth filter
[h6pole,freq6] = freqs(b6pole,a6pole,4096); %Calculate Frequency Response
%Plot frequency response
loglog(freq2/(2*pi),abs(h2pole));
hold on
loglog(freq6/(2*pi),abs(h6pole));
xlabel('Frequency (Hz)');
ylabel('Magnitude');
legend('2 Pole Butterworth', '6 Pole Butterworth')
As you can see, as we increase the number of poles in our filter the closer it gets to our perfect filter. Or in electronic engineering terms, it has a steeper “roll off”. You might ask “well then why don’t we use 1 million pole filters then?”. Well digitally, we can create very high order filters. However, when it comes to real circuits there are a bunch of reasons why this is difficult, one of which is that it becomes very difficult to find resistors and capacitors of the exact correct value needed. Another reason is that by the time you get up to 8 poles, that is usually good enough. For instance, with an 8 pole Butterworth filter, you attenuate a signal at twice the corner frequency to about 4% of it’s original value. At 10x the corner frequency, the signal is attenuated by about 1 billion fold. But the important thing to note is that even with a filter with a large number of poles it does not remove ALL of the signal above the corner frequency.
Butterworth?
%All our filters will have a corner
%frequence (fc) of 1000 Hz
fc = 1000; % Corner Frequency of
n_poles = 8;
[zbess, pbess, kbess] = besself(n_poles, 2*pi*fc); %Create 8 pole Bessel
[bbess,abess] = zp2tf(zbess,pbess,kbess); %Convert to transfer function
[hbess,freqbess] = freqs(bbess,abess,4096); %Calculate Frequency Response
[bbut,abut] = butter(n_poles,2*pi*fc,'s'); %Create a 8 butterworth filter
[hbut,freqbut] = freqs(bbut,abut,4096); %Calculate Frequency Response
[bcheb,acheb] = cheby1(n_poles,3,2*pi*fc,'s'); %Create 8 pole Chebychev cheby1(n,3,2*pi*f,'s');
% with 3dB of ripple
[hcheb,freqcheb] = freqs(bcheb,acheb,4096); %Calculate Frequency Response
%Plot frequency response
figure;
loglog(freqbess/(2*pi), abs(hbess))
hold on
loglog(freqbut/(2*pi),abs(hbut));
loglog(freqcheb/(2*pi),abs(hcheb));
xlabel('Frequency (Hz)');
ylabel('Magnitude');
legend('Bessel', 'Butterworth', 'Chebychev')
xlim([10 10000])
ylim([10^-4 2])
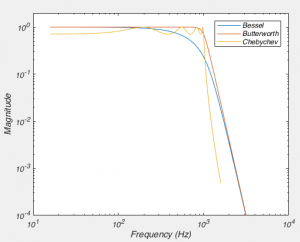
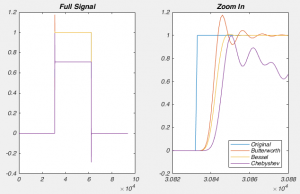
However, when comparing the Bessel and the Butterworth, it may seem like the Butterworth is clearly superior: The Bessel filter attenuates signals below the corner frequency just like the Chebyshev! But when you look in the time domain, the reason why physiologists nearly always use a Bessel filter becomes obvious. Other filters producing “ringing” after encountering a step-like response. This is because the other filters delay waves of different frequencies by different times (remember, a step like response is created by a sum of a large number of waves). However, the Bessel filter doesn’t do this. The technical way to describe this is that a Bessel filter has linear phase response. This doesn’t mean it affects the phase of all the frequencies in the pass band equally, but that the way if shifts the phase means that the various frequency components aren’t shifted in time by different amounts (think about the fact that one cycle of a slow wave lasts for longer than a faster wave, so if both waves were shifted by half a wave, then slow wave would be shifted by more time). It turns out the Bessel filter is the best possible way to achieve this.
Digitizing – The hidden filter
%% Original, high sample rate signal
% Let us imagine this is like our analog signal
nfft = 4096;
dt = 0.001; % inter sample time = 0.001s = 1kHz sampling
t = (1:nfft)*0.001; % time vector
% Create signal vector that is the sum of 32 Hz, 64 Hz, and 256 Hz
signal = sin(32*2*pi*t) + sin(2*pi*64*t) + sin(2*pi*256*t);
f = (1/dt)/2*linspace(0,1,nfft/2+1)'; %Create Frequency vector
dft = fft(signal, nfft)/(length(signal)/2); % take the FFT of original
mag = abs(dft(1:nfft/2+1)); %Calculate magnitude
semilogx(f, mag, 'LineWidth', 2 );
%% Now lets digitize our faux-analog signal
% Essentially we are down sampling,
% by sampling it every 0.005s = 200 Hz = every 5th sample.
signal_dig = signal(1:5:end);
nfft_dig = 2^nextpow2(length(signal_dig)); %FFTs are faster if you perform them
%on power of 2 lengths vectors
f_dig = (1/(dt*5))/2*linspace(0,1,nfft_dig/2+1)'; %Create Frequency vector
dft_dig = fft(signal_dig, nfft_dig)/(length(signal_dig)/2);
mag_dig = abs(dft_dig(1:nfft_dig/2+1));
hold on
semilogx(f_dig, mag_dig, 'LineWidth', 2);
xlim([10 1000])
xlabel('Frequency (Hz)');
ylabel('Magnitude');
legend('Original Signal', 'Digitized Signal');
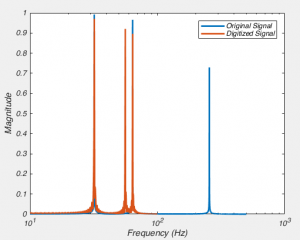
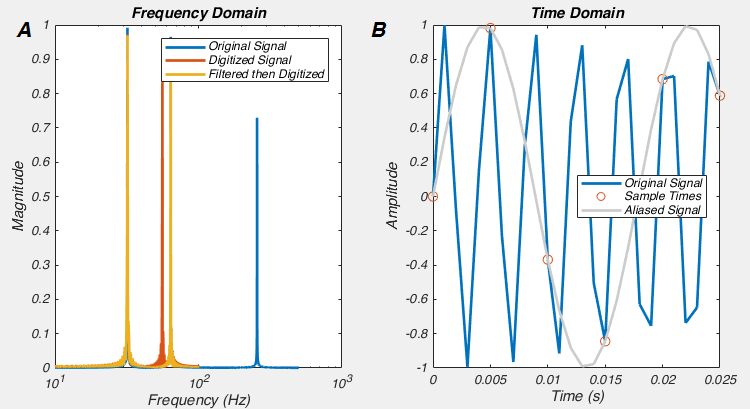
In the code, we create a signal that is a sum of 32, 64 and 256 Hz sine waves. We’ll think of this signal as being our analog signal. We then “digitize” it as 200 Hz. We then look at the two signals in the frequency domain. In the original signal we see peaks at 32, 64 and 256 Hz, and after we digitize it at 200 Hz, we see a loss of 256 Hz signal, which perhaps isn’t too surprising when you think about it. But something very disturbing has happened, we now have a new signal with a peak at 56 Hz. This signal is a complete phantom and is called “Aliasing”, and it happened because we need to filter before we digitize (See Fig 9B). This is a correlate of the Nyquist-Shannon sampling theorem, which says that any signal which has no frequency component higher than F, can be perfectly reconstructed if it is sampled at 2F. So, inversely, if we digitize a signal at rate 2F, but it has frequency components higher than F, then the digitized signal we end up with is not a faithful representation of the original. Now let’s try to follow the rules. If we add in these lines of code, then we get Fig 9A.
%% Let's filter the signal before we digitize it [bbut,abut] = butter(8,100/(1000/2)); %Create a 100Hz, 8 pole butterworth filter signal_filt = filter(bbut, abut, signal); %Filter the data signal_filt_dig = signal_filt(1:5:end); dft_filt_dig = fft(signal_filt_dig, nfft_dig)/(length(signal_filt_dig)/2); mag_filt_dig = abs(dft_filt_dig(1:nfft_dig/2+1)); semilogx(f_dig, mag_filt_dig, 'LineWidth', 2);
And this is one of the two reasons why we must ALWAYS low-pass filter data before we digitize it: if we don’t, we will get aliases, i.e. spurious frequency components. This is also what causes strange patterns in some photographs, the original data had higher frequencies (i.e. patterns changing in space) than the camera CCD could sample. The other reason we filter BEFORE was digitize is that high frequency noise can sometimes be larger than the signal we want to record, and hence filtering before digitization allows us to amplify the signal as much as possible without saturating the digitizer.
Choosing a corner and sampling frequency
dt = 1/20000; % 20kHz sampling rate
t = 0:dt:0.02; % time vector 4ms long
signal = exp(-(t-0.01).^2/(0.001/sqrt(2*log(2)))^2); %Gaussian with 1ms FWHM
nfft = 2^nextpow2(length(signal)); %FFTs are faster if you perform them
%on power of 2 lengths vectors
f = (1/dt)/2*linspace(0,1,nfft/2+1)'; %Create Frequency vector
dft = fft(signal, nfft)/(length(signal)/2); %take the FFT of original
mag = abs(dft(1:nfft/2+1)); %Calculate magnitude
subplot(1,2,1);
semilogx(f, mag, 'LineWidth', 2);
title('Freq Components of Original')
xlabel('Frequency (Hz)');
ylabel('Magnitude');
xlim([30 10000]);
xticks([100, 1000, 10000]);
[bbess, abess] = besself(8, 2*pi*1000); %Create 8 pole 1kHz filter
[num,den] = bilinear(bbess,abess,1/dt);
signalbess1k = filter(num, den, signal); %Apply Filter
[bbess, abess] = besself(8, 2*pi*5000); %Create 8-pole 5kHz filter
[num,den] = bilinear(bbess,abess,1/dt);
signalbess5k = filter(num, den, signal); %Apply Filter
subplot(1,2,2);
plot(t*1000,signal, t*1000, signalbess1k, t*1000, signalbess5k, 'LineWidth', 2);
xlabel('Time (ms)')
ylabel('Amplitude')
legend('Original Signal', 'Filtered Signal (1kHz)', 'Filtered Signal (5kHz)', 'Location', 'south');
I should probably add that these rules of thumb are not absolute (apart from digitizing at greater than twice your filter rate: always do that!). If your filter slightly deforms the shape of your action potential, or slightly delays it in time, this may not matter for your particular experiments. But you should still be aware of the fact that if you’re filtering too close to your signal of interest, you are not recording the “true” signal.
Conclusion/Rules of Thumb
- A filter removes unwanted frequeny components
- A low-pass filter removes high frequency signals
- A filter with more poles has a steeper roll off
- A Bessel filter has the best behaviour in the time domain
- For a 4-pole Bessel, you must filter at at least 4 times the frequency of the fastest wanted component of your signal
- For an 8-pole Bessel, you must filter at at least 5 times the frequency of the fastest wanted component of your signal
- You must digitize at more than 2-3 times the frequency of your low-pass filter

Hi, I came across this while looking up how to design filters. i have a question. What if we use the “filtfilt” command instead of “filter”. Matlab documentation says that it compensates for the delay introduced by the filter.
Yes, filtfilt filters the signal first in the normal direction, going forward in time (which delays signals in time), the it takes that filtered signal and filters it again in the reverse direction, going backwards in time (which advances signals in time). This second filtering essentially undoes the time delay caused by the first filter. It also means the filter has double the number of poles of the filter you specified.
Actually, not a bad idea for a blog post seeing as how common filtfilt is just used by default.